वृत के अंदर बनी आकृति के कोण और भुजा निकालना – Circles class 10 extra questions

Circles class 10 extra questions मे वृत के अंदर बने त्रिभुज, चतुर्भुज और बहुभुज के कोणों और भुजाओ को निकालना सीखेंगे निम्नलिखित 18 सवालो को चित्र सहित हल किया गया है –

Circles class 10 extra questions –

वृत्त पर आधारित प्रथम 20 प्रश्न – https://www.examhelp4.com/circle-based-questions/

Q1. दिए गये चित्र में PQRS एक चक्रीय चतुर्भुज है तथा POQ इस वृत्त का व्यास है यदि ∠QRS = 150° हो, तो ∠SQP का मान कितना है

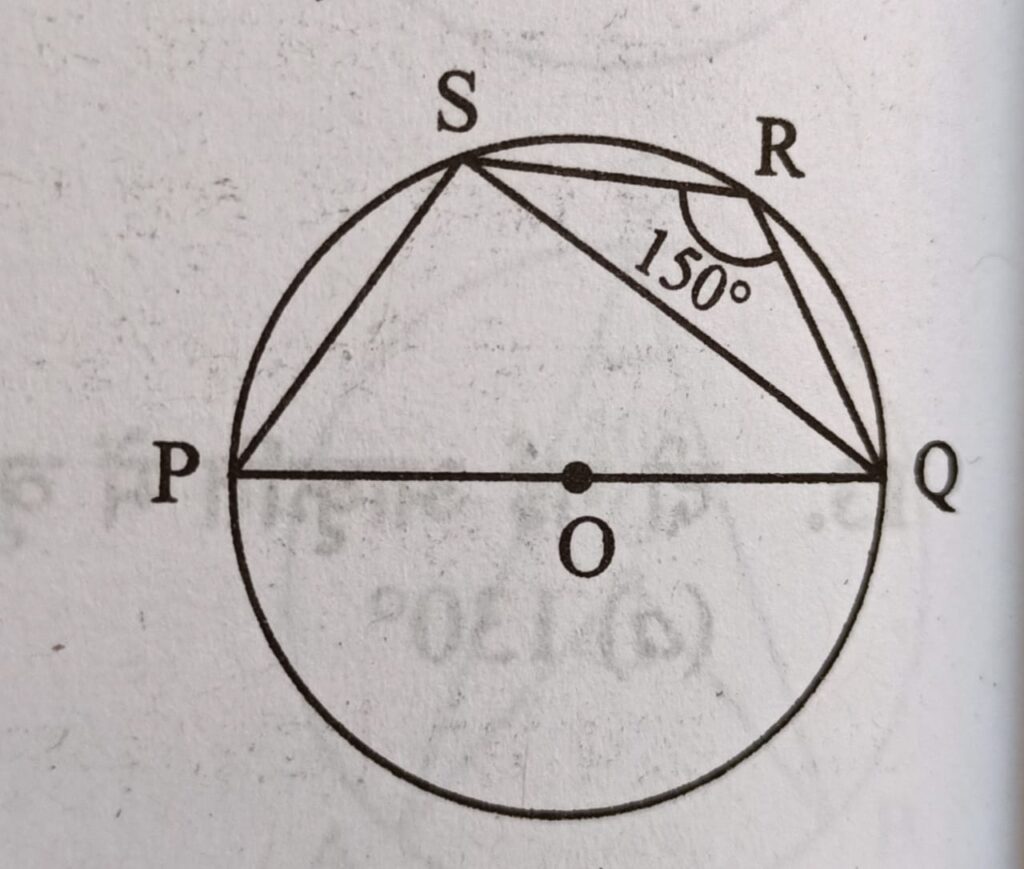
∠QRS + ∠QPS = 180° वृत्त के अंदर बने चतुर्भुज के आमने सामने के कोणों का योग

150 + ∠QPS = 180° ⇒ ∠QPS = 30°

∠PSQ = 90 अर्धवृत में बना कोण

त्रिभुज QPS में,

∠PQS + ∠QSP + ∠SPQ = 180°

∠PQS + 90 + 30 = 180° ⇒ ∠PQS = 60°

Q2. दी गई आकृति में वृत्त का केंद्र O है यदि ∠AOC = 90° तथा ∠AOB = 110° हो, तथा ∠BAC = x हो, तो x का मान क्या होगा ?

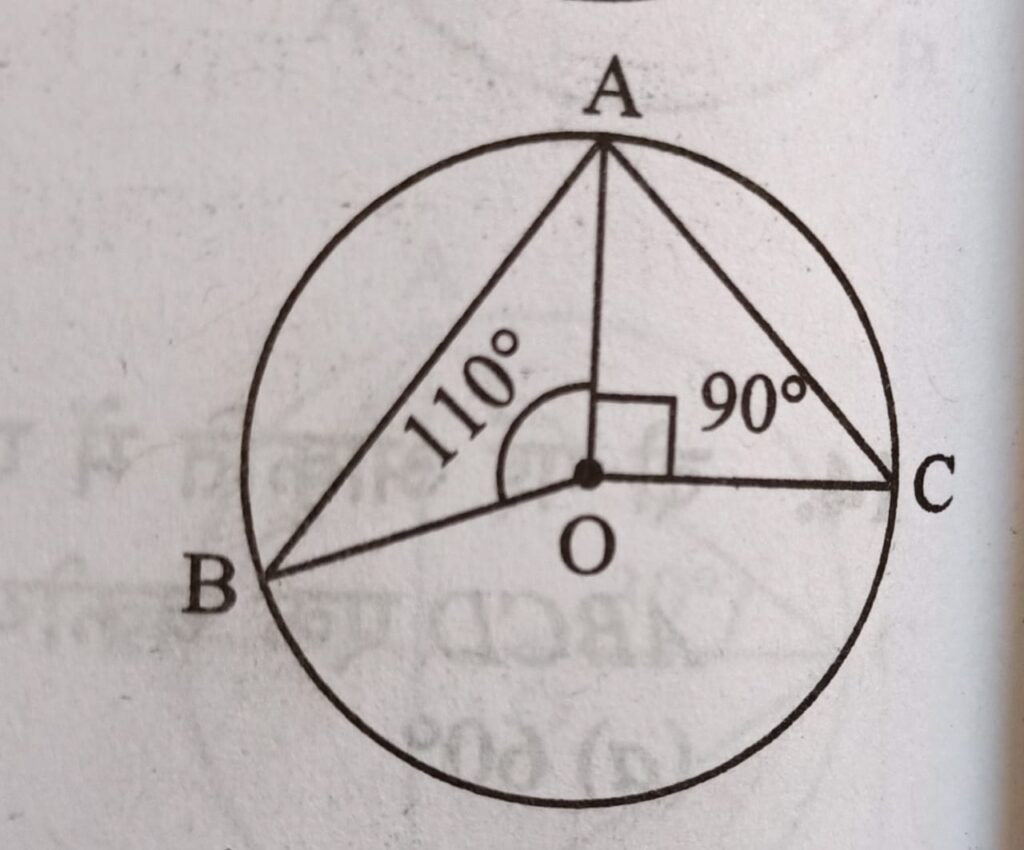
∠BOC + ∠BOA + ∠COA = 360°

∠BOC + 110 + 90 = 360 ⇒ ∠BOC = 120°

∠BAC = (1/2)∠BOC ⇒ ∠BAC = 60°

Q3. दी गई आकृति में वृत्त के बाहर बिंदु P से जीवाये PA तथा PC खीची गई है यदि PA = 8 cm, PD = 4 cm तथा CD = 3 cm हो, तो AB की लम्बाई कितनी है

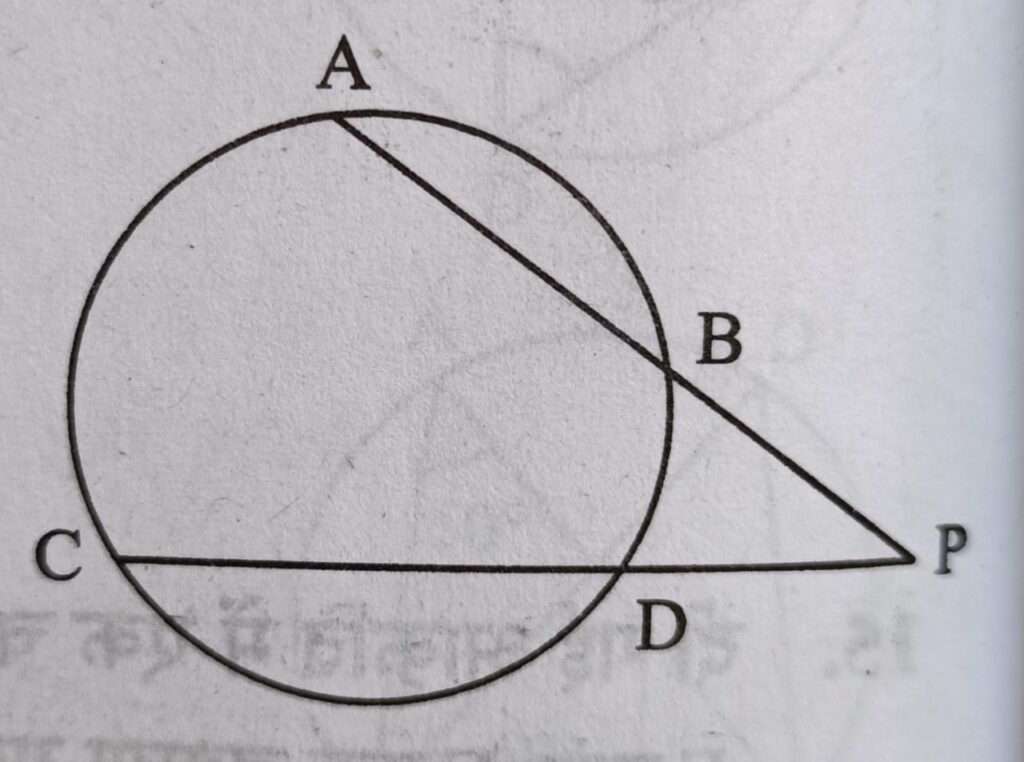
माना AB = x cm, तब PB = 8 – x

PA × PB = PC × PD

8 × (8 – x) = 7 × 4 ⇒ 64 – 8x = 28

8x = 36 ⇒ x = 4.5

Q4. किसी वृत्त की दो जीवाये AB तथा CD एक- दुसरे को बिंदु E पर काटती है यदि AE = 4 cm, EB = 6 cm तथा CE = 5 cm हो तो ED का नाप कितना होगा ?

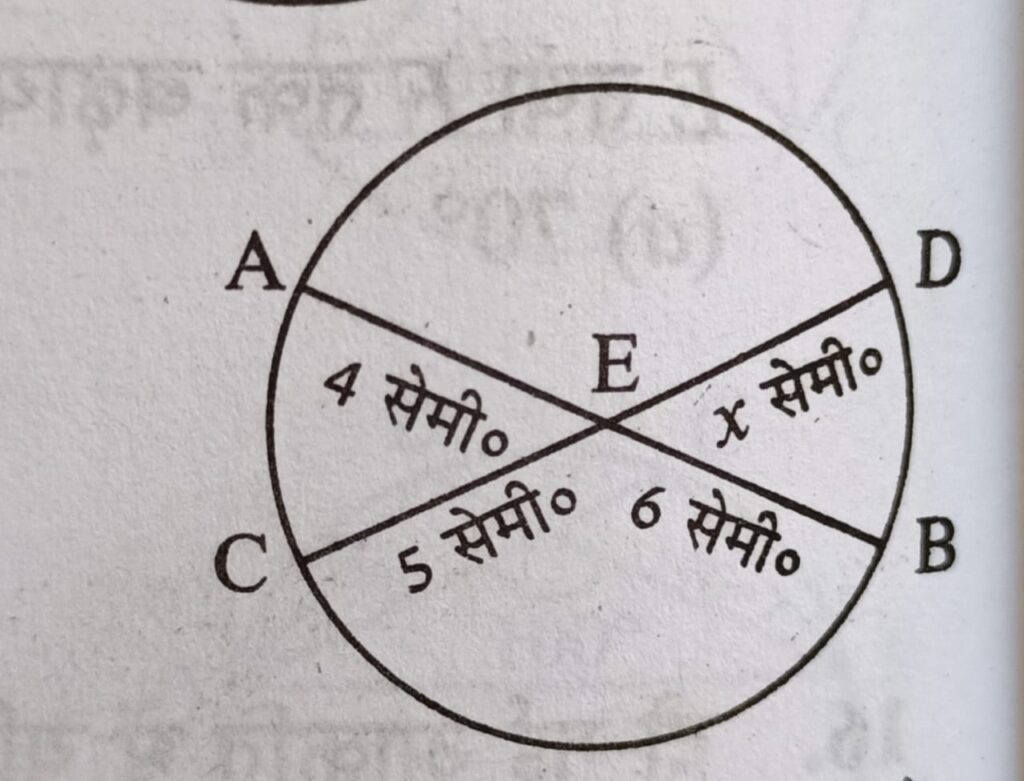
AE × EB = CE × ED

4 × 6 = 5 × x ⇒ x = 4.8 cm

Q5. ΔABC के शीर्षों को केंद्र मान कर तीन वृत्त खीचे जाते है जिनमे से प्रत्येक अन्य दो को बाह्य स्पर्श करता है यदि त्रिभुज की भुजाये 4 cm, 6 cm तथा 8 cm लम्बी हो, तो तीनों वृतो की त्रिज्याओ का योग कितना होगा ?

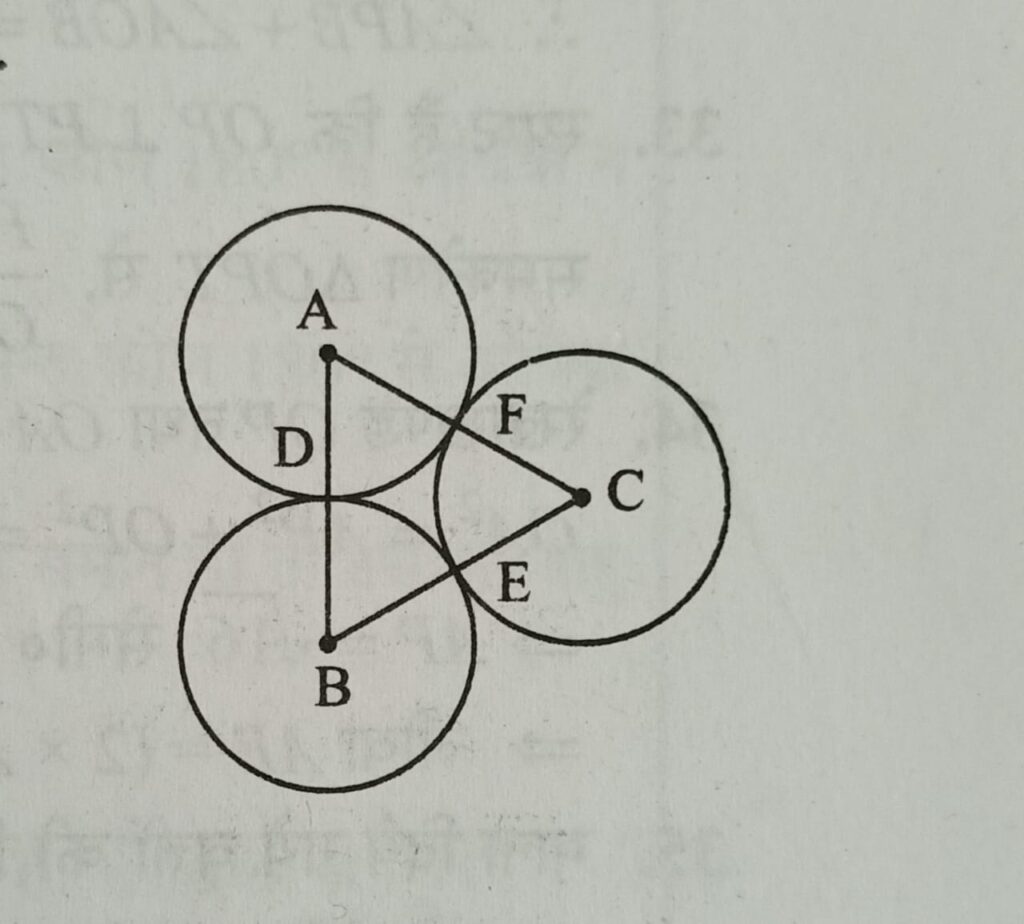
माना AD = r₁, BE = r₂, CF = r₃

तब r₁ + r₂ = 4 क्योकि AB = 4 …………………. 1

r₂ + r₃ = 6 क्योकि BC = 6 …………………. 2

r₃ + r₁ = 8 क्योकि AC = 8 …………………. 3

2(r₁ + r₂ + r₃) = 18 ⇒ (r₁ + r₂ + r₃) = 9

तीनों वृतो की त्रिज्याओ का योग = 9 cm

Q6. 10 cm त्रिज्या के वृत्त के अंतर्गत एक समकोण त्रिभुज बनाया गया है वृत्त का व्यास त्रिभुज की एक भुजा है तथा त्रिभुज की परिमिति 48 cm है इस त्रिभुज की अन्य दो भुजाओ की माप क्या है ?

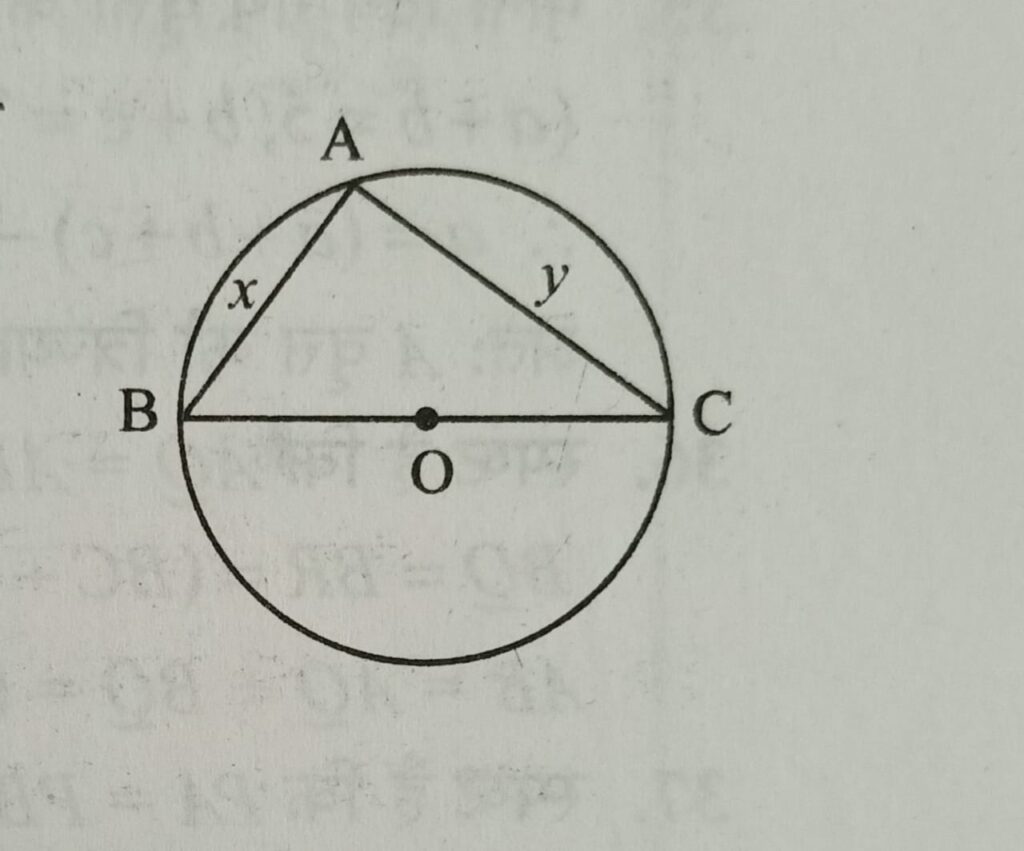
माना समकोण त्रिभुज ABC की भुजा AB = x और भुजा AC = y है तब

x + y + BC = 48 क्योकि त्रिभुज की परिमिति 48 cm है

x + y = 28 (क्योकि BC = 2×10) …………………… 1

समकोण त्रिभुज ABC में,

x² + y² = (20)² ⇒ x² + y² = 400 …………………… 2

x² + y² + 2xy = 784 …………………… 3

समीकरण 2 और 3 से,

xy = 192 cm

(x – y)² = x² + y² – 2xy = 400 – 384 = 16

(x – y) = 4 …………………… 4

समीकरण 1 और 4 से,

x = 16 और y = 12

Q7. एक फर्श की वृताकार परिधि पर तीन लड़के खडे है वे एक-दुसरे से समान दूरी पर है यदि फर्श की त्रिज्या 5 मीटर हो तो दो लडकों के बीच न्यूनतम दूरी कितनी है ?

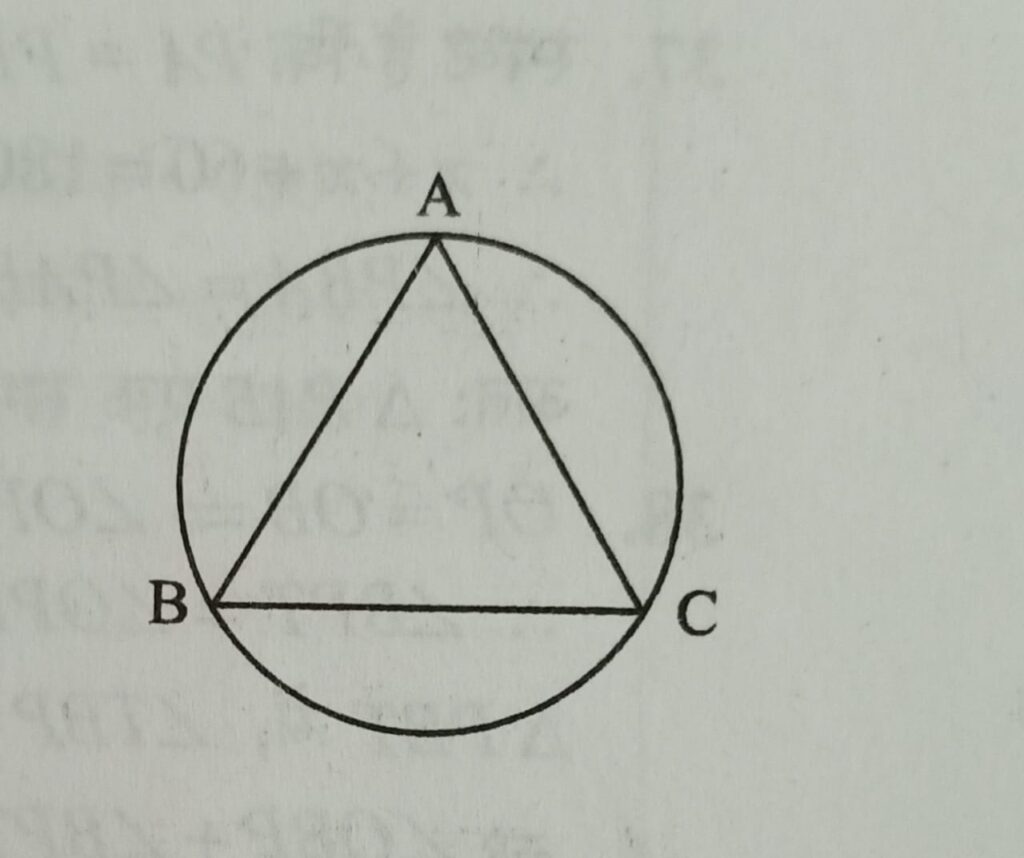
फर्श की वृताकार परिधि पर तीन लड़के खड़े होने से बना समबाहु त्रिभुज ABC का क्षेत्रफल = [(√3)/4] a²

(AB × BC × CA)/4r = [(√3)/4] a² ⇒ (a × a × a)/4r = [(√3)/4] a²

a/r = (√3) ⇒ a = 5√3 [क्योकि r = 5]

दो लडकों के बीच न्यूनतम दूरी = 5√3

Q8. दी गई आकृति में ABCD एक चक्रीय चतुर्भुज है जिसमे DC को E तक बढ़ाया गया है तथा CF ∥ AB खीचा गया है यदि ∠ADC = 95° तथा ∠ECF = 20° हो, तो ∠BAD का माप क्या होगा ?

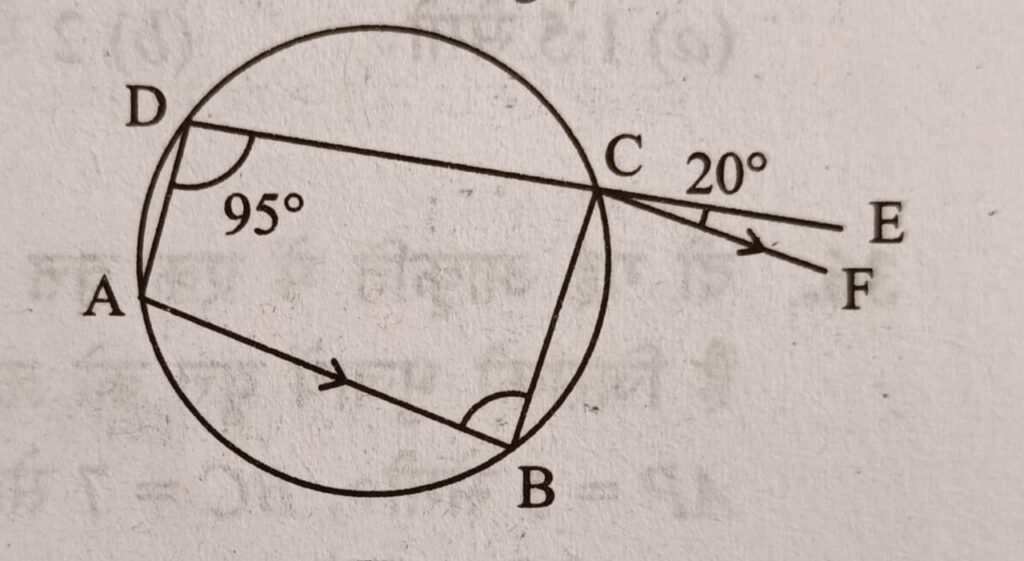
∠ABC + ∠ADC = 180 ⇒ ∠ABC + 95 = 180

∠ABC = 85

∴ ∠BCF = 85 [∵ एकांतर कोण (∠ABC = ∠BCF)]

∠BCE = ∠BCF + 20 ⇒ ∠BCE = 105

∠BCD + ∠BCE = 180 ⇒ ∠BCD = 75

∠BAD + ∠BCD = 180° [∵ सर्किल के अंदर बने चतुर्भुज के आमने सामने के कोणों का योग]

∴ ∠BAD = 105°

Q9. दिये गये वृत्त का केंद्र O है O से 10 cm दूरी पर एक बिंदु P लिया गया है इस बिंदु से वृत्त पर स्पर्श रेखा PT खीची गई है यदि PT = 8 cm हो, तो वृत्त की त्रिज्या कितनी है ?

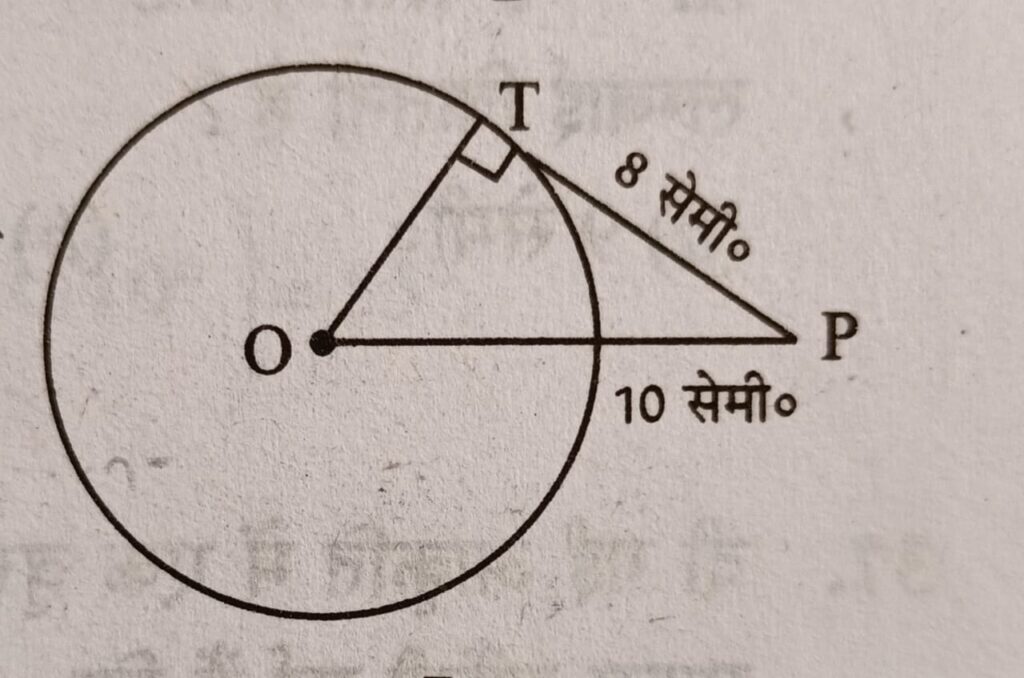
समकोण त्रिभुज PTO में,

PO² = PT² + TO² ⇒ 100 = 64 + TO²

TO² = 36 ⇒ TO = 6 cm

Q10. दिये गये चित्र में एक वृत्त का केंद्र O है केंद्र से 26 cm दूरी पर स्थित बिंदु P से स्पर्श रेखा PT खीची गई है यदि वृत्त की त्रिज्या 10 cm हो तो PT की लम्बाई कितनी है ?

समकोण त्रिभुज PTO में,

PO² = PT² + TO² ⇒ 676 = PT² + 100

PT = 24 cm