Important Properties of Circles in Hindi को पढने के बाद Circle important Questions class 10 को आप बड़ी ही आसानी से हल कर सकते हो –

Circle important Questions class 10 – वृत्त पर आधारित 17+ प्रश्न:-
Q1. एक वृत्त की त्रिज्या 10 cm है तथा इस वृत्त की एक जीवा की लम्बाई 12 cm है इस जीवा की केंद्र से दूरी कितनी है ?
हल :- AB = 12 cm, OA = OB = 10 cm [क्योकि दिया है]
हमे ज्ञात करना है (OL) = ?
बिंदु O को A से और B से मिलाने पर त्रिभुज OAB में हमे दो समकोण त्रिभुज OLB और OLA प्राप्त होती है
समकोण त्रिभुज OLB में,
(OL)2 + (LB)2 = (OB)2
(OL)2 + (6)2 = (10)2 [∵ OL ⊥ AB]
(OL)2 = 100 – 36 = 64 ⇒ OL = 8
जीवा की केंद्र से दूरी (OL) = 8
Q2. एक वृत्त के केंद्र से 12 cm की दूरी पर 32 cm लम्बी जीवा खीची गई है इस वृत्त की त्रिज्या कितनी है
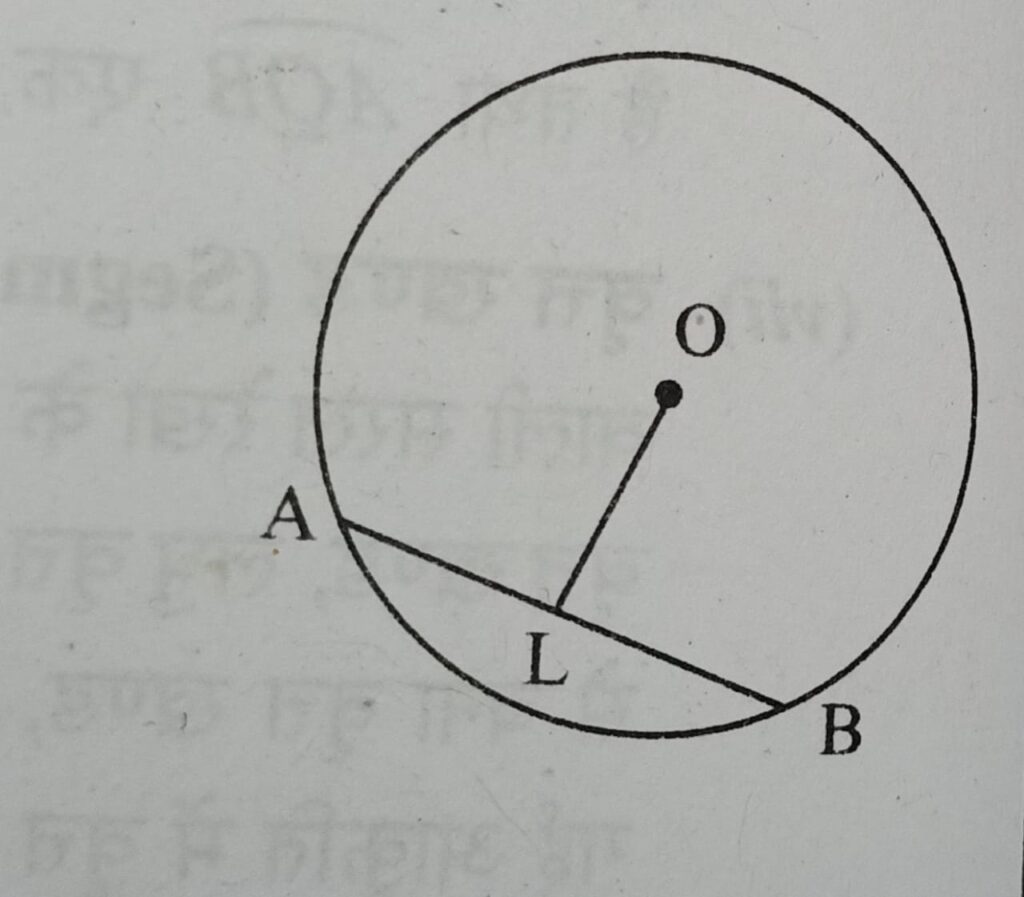
हल :- OL = 12 cm, AB = 32 cm [क्योकि दिया है]
हमे ज्ञात करना है OA = OB = ?
बिंदु O को A से और B से मिलाने पर त्रिभुज OAB में हमे दो समकोण त्रिभुज OLB और OLA प्राप्त होती है
समकोण त्रिभुज OLB में,
(OL)2 + (LB)2 = (OB)2
(12)2 + (16)2 = (OB)2
(OB)2 = 400
वृत्त की त्रिज्या = OB = 20 cm
Q3. दी गई आकृति में वृत्त का केंद्र O है, AB वृत्त की एक जीवा है तथा BC वृत्त का व्यास है यदि OD ⊥ AB हो, तथा OD = 4 cm तब AC की लम्बाई कितनी होगी ?
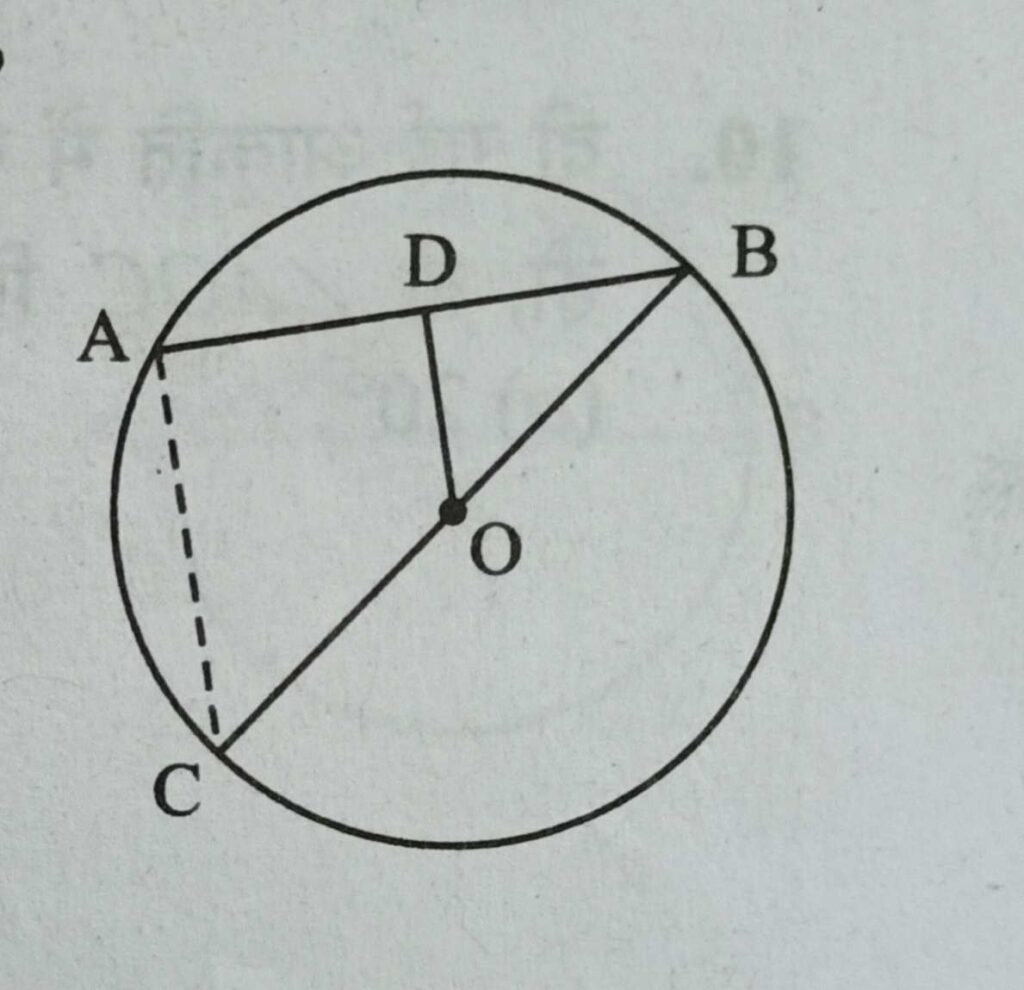
हल :- त्रिभुज BAC में,
D तथा O क्रमशः BA तथा BC के मध्य बिंदु है
अत DO ∥ AC तथा DO = (1/2)AC
(1/2)AC = 4 ⇒ AC = 8 cm
Q4. दी गई आकृति में वृत्त का केंद्र O है, AB तथा CD इसकी दो बराबर जीवाये है यदि ∠AOB = 70° है, तो ∠COD का मान क्या होगा ?
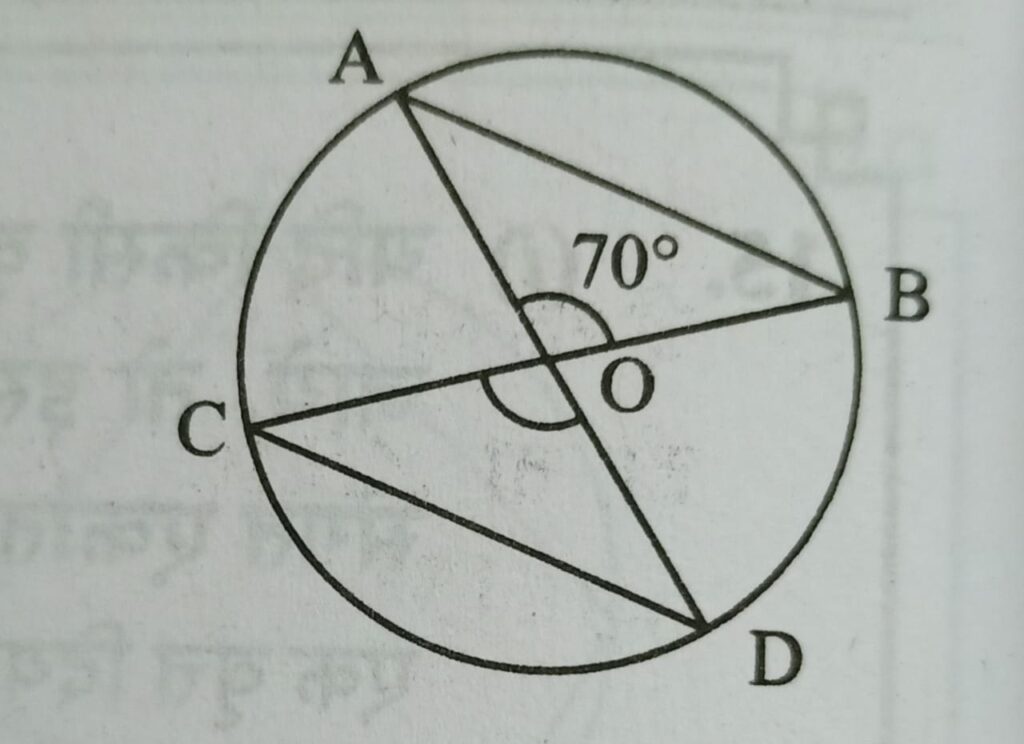
हल :- AB ∥ CD [∵ AB तथा CD इसकी दो बराबर जीवाये है]
∠AOB = 70° = ∠COD [∵ वृत्त की समान जीवाये वृत्त के केंद्र पर समान कोण बनाती है
Q5. दी गई आकृति में वृत्त का केंद्र O है यदि ∠OAB = 35° हो तथा C वृत्त पर कोई बिंदु लिया गया हो, तो ∠ACB = ?
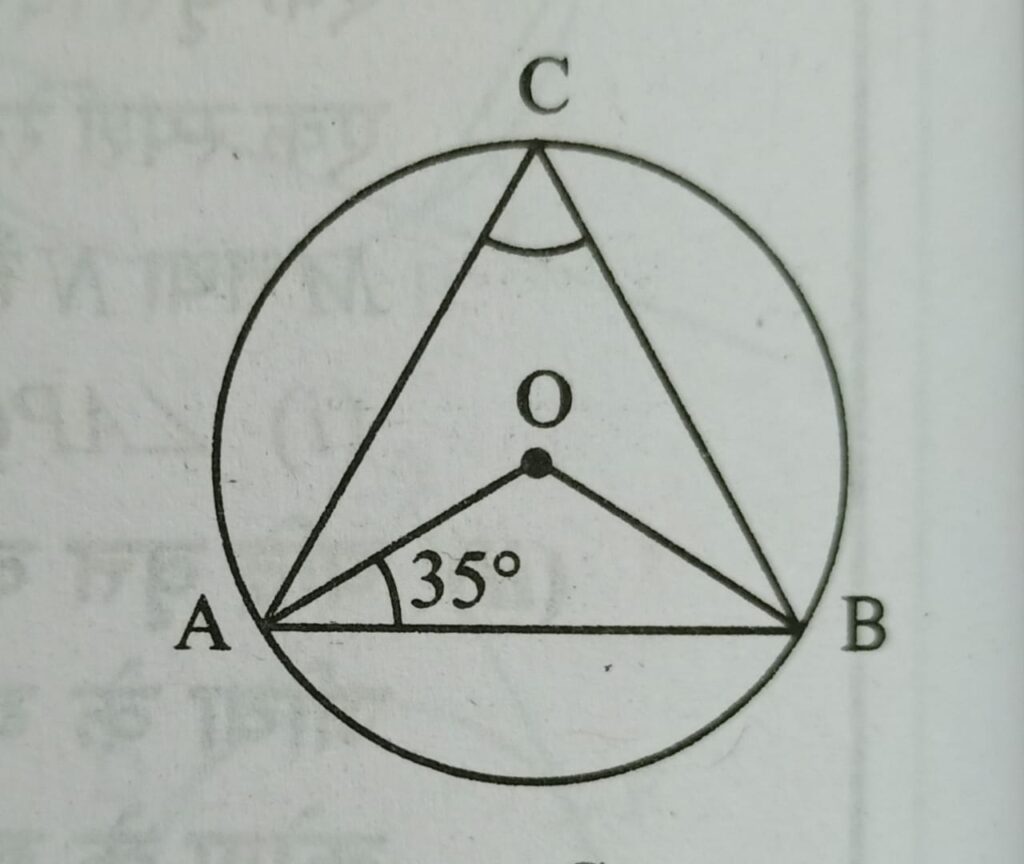
हल :- त्रिभुज AOB में,
∠OAB = 35° = ∠OBA [∵ OA = OB]
और ∠BOA = 180 – 70 = 110° [∵ ∠OAB + ∠ABO + ∠BOA = 180°]
∠ACB = (1/2)∠BOA
∠ACB = 55°
Q6. दी गई आकृति में वृत्त का केंद्र O है तथा ∠ACB = 40° है तब ∠AOB = ?
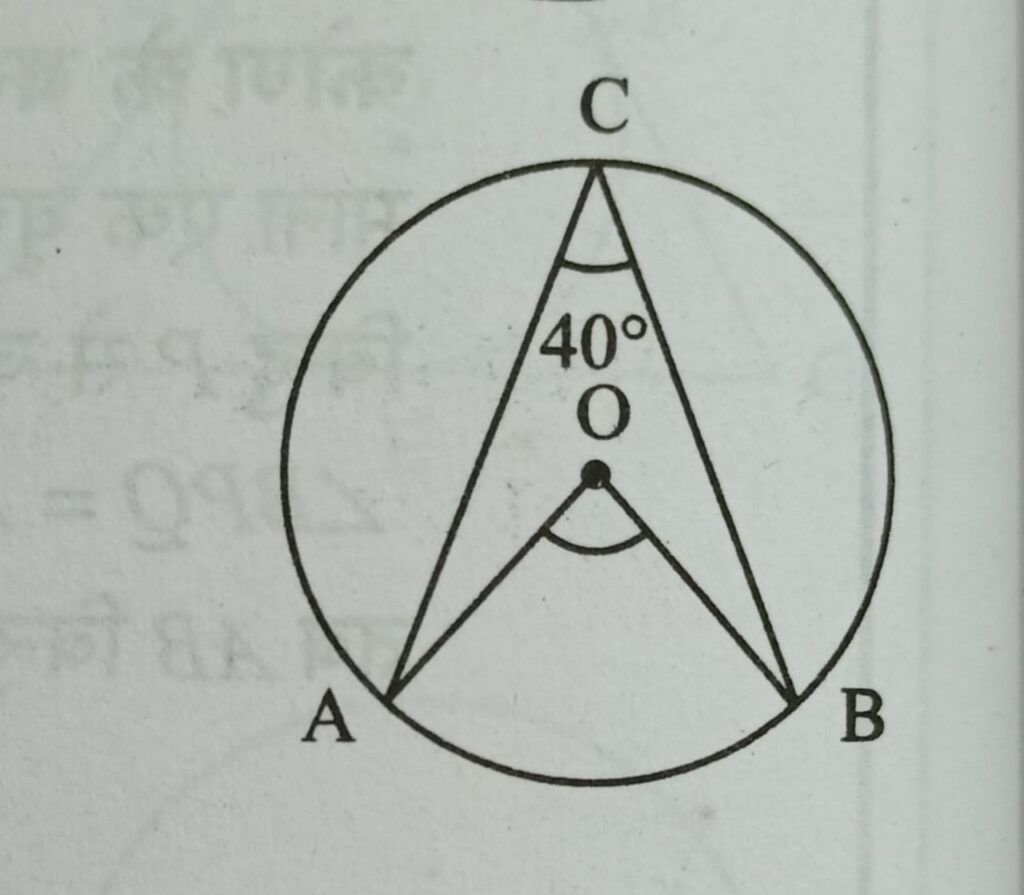
हल :- ∠ACB = (1/2)∠AOB ⇒ 40 = (1/2)∠AOB
∠AOB = 80°
Q7. दी गई आकृति में वृत्त का केंद्र O है तथा BOC इस वृत्त का एक व्यास है यदि ∠BCA = 30° हो, तो ∠CDA = ?
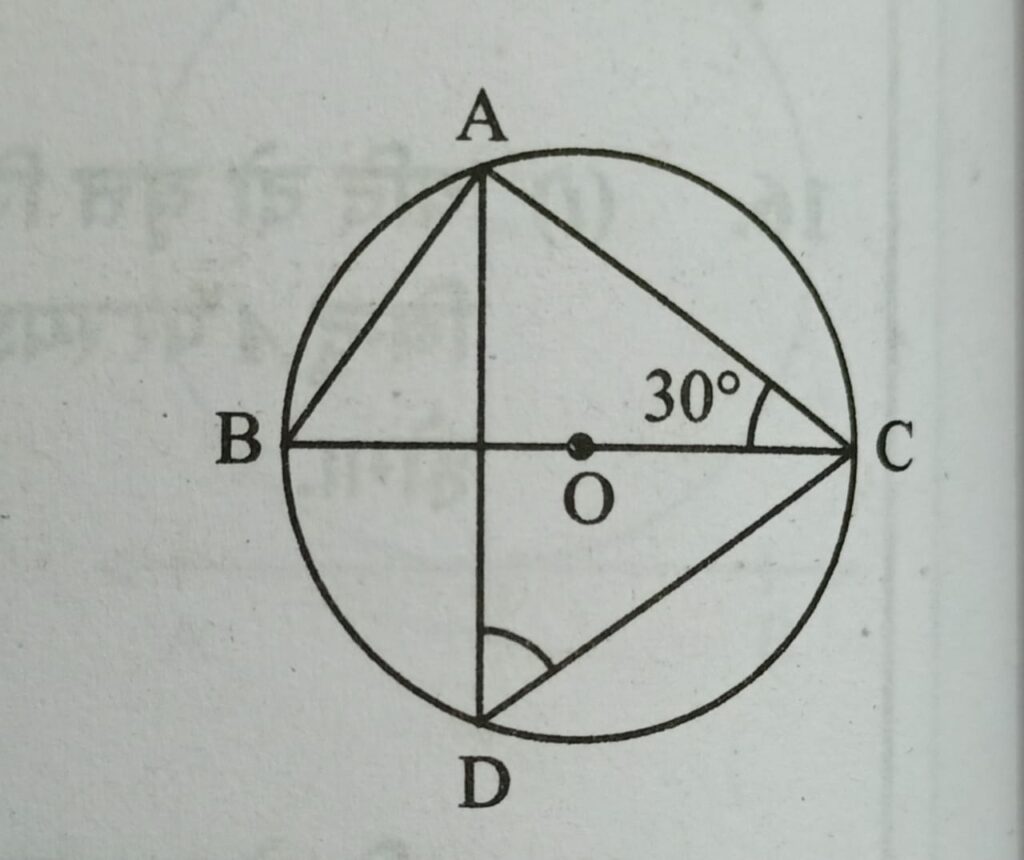
हल :- जहा पर AD और BC आपस में काटते है माना वह बिंदु E तब,
समकोण त्रिभुज AEC में,
∠EAC = 60° [∵ ∠A + ∠E + ∠C = 180]
∠CDA = 60° [∵ ΔAEC ≅ ΔDEC]
Q8. दी गई आकृति में ΔABC तथा ΔDBC का परिवृत खीचा गया है जो इस प्रकार है कि ∠BAC = 50° तथा ∠DBC = 60° तब ∠BCD = ?
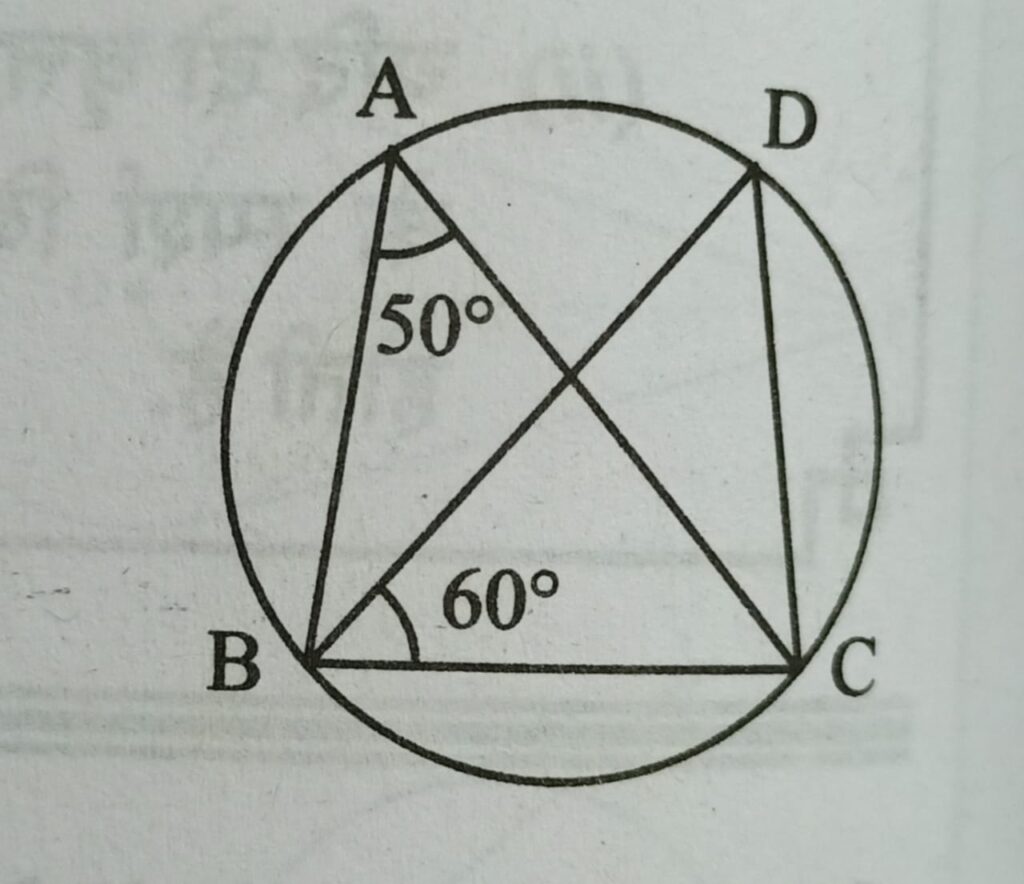
हल :- ΔABC ≅ ΔDCB इसलिए ∠BDC = 50°
अब त्रिभुज DCB में,
∠D + ∠C + ∠B = 180° ⇒ 50° + ∠C + 60° = 180°
∠C = 70° ie. ∠BCD = 70°
Q9. दी गई आकृति में वृत्त का केंद्र O है तथा जीवाये AC तथा BD बिंदु E पर काटती है यदि ∠AEB = 100° तथा ∠CBE = 30° हो, तो ∠ADB = ?
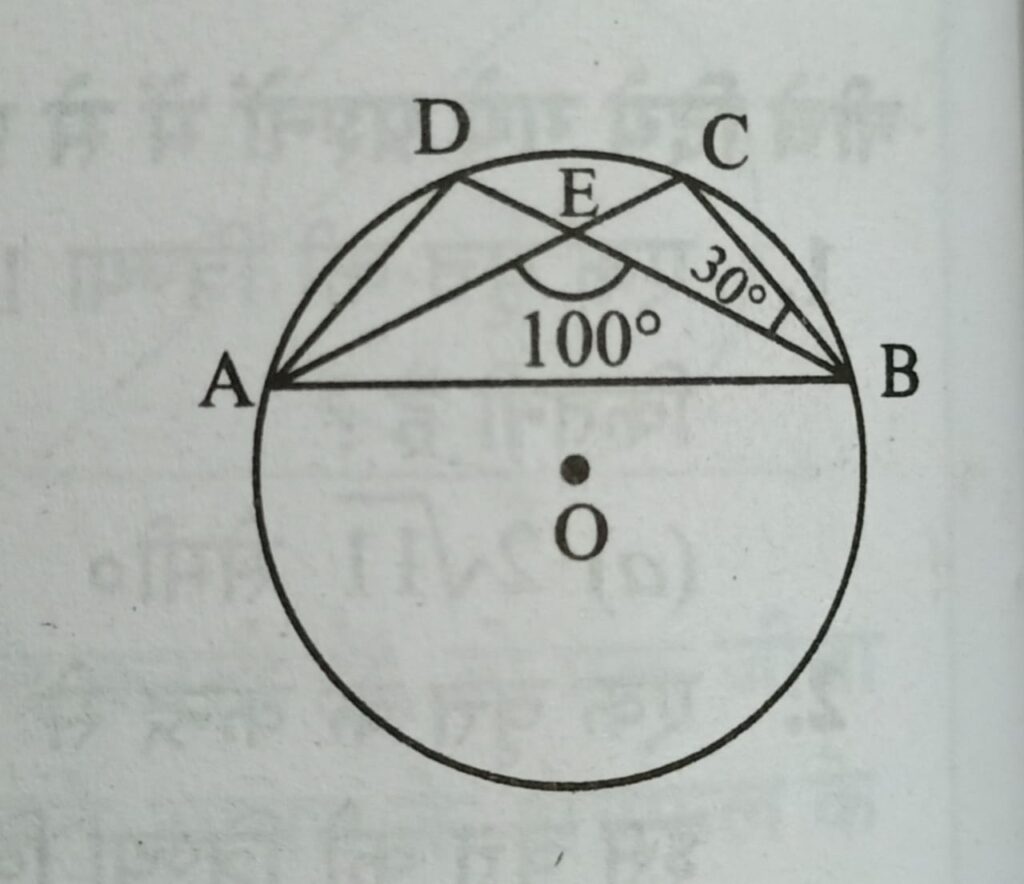
हल :- ΔBCA ≅ ΔADB इसलिए ∠CBE = ∠DAE = 30°
अब त्रिभुज AEB में, (STEP 1)
∠EAB + ∠ABE + ∠BEA = 180° क्योकि त्रिभुज के तीनो कोणों का योग 180 होता है
x + 100° + x = 180° [∵ ∠EAB = ∠BEA]
2x = 80° ⇒ x = 40°
∠CBA = ∠EBA + ∠CBE ⇒ ∠CBA = 70°
अब त्रिभुज CBA में, (STEP 2)
∠CBA + ∠BAC + ∠ACB = 180° क्योकि त्रिभुज के तीनो कोणों का योग 180 होता है
70 + 40 + ∠ACB = 180° ⇒ ∠ACB = 70°
∠ADB = ∠ACB = 70° [∵ ΔBCA ≅ ΔADB]
Q10. दी गई आकृति में वृत्त का केंद्र O है, ∠OAB = 30° तथा ∠OCB = 50° हो, तो ∠AOC कितना होगा ?
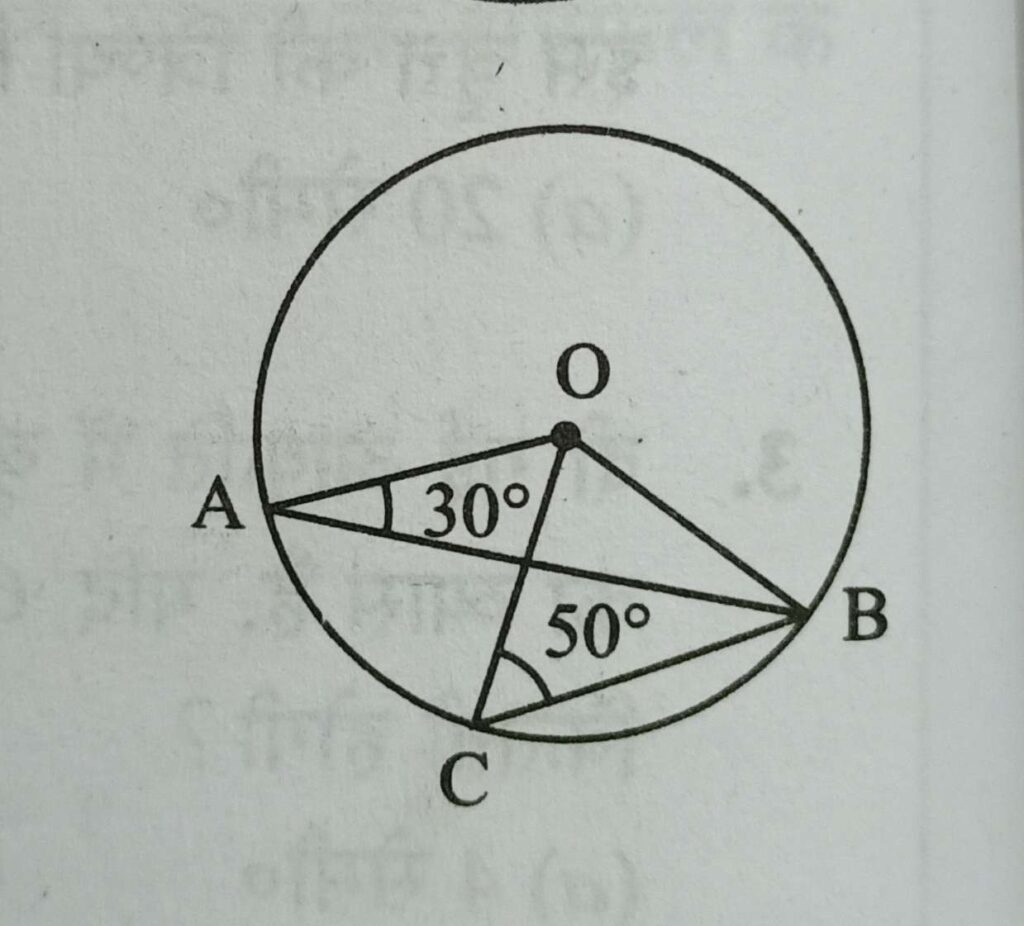
हल :- त्रिभुज AOB में,
∠OAB + ∠ABO + ∠BOA = 180°
30 + 30 + ∠BOA = 180 [∵ OA = OB]
∠BOA = 120 और इसी प्रकार
त्रिभुज OCB में, ∠COB = 80°
∠AOC + ∠COB = 120 ⇒ ∠AOC = 40°



