त्रिभुज की सर्वांगसमता के नियम

त्रिभुज की सर्वांगसमता के नियम में दिए गए महत्वपूर्ण RHS सर्वांगसमता नियम, थेल का प्रमेय जिससे congruence of triangles class 9, 10 तक के सभी सवालो को हल कर सकते है –

समरूप में एक जेसा रूप होता है लेकिन इनके आकार में अंतर पाया जाता है और अगर एक जेसा रूप और आकार पाया जाता है तो उसे हम सर्वांगसम कहेंगे-

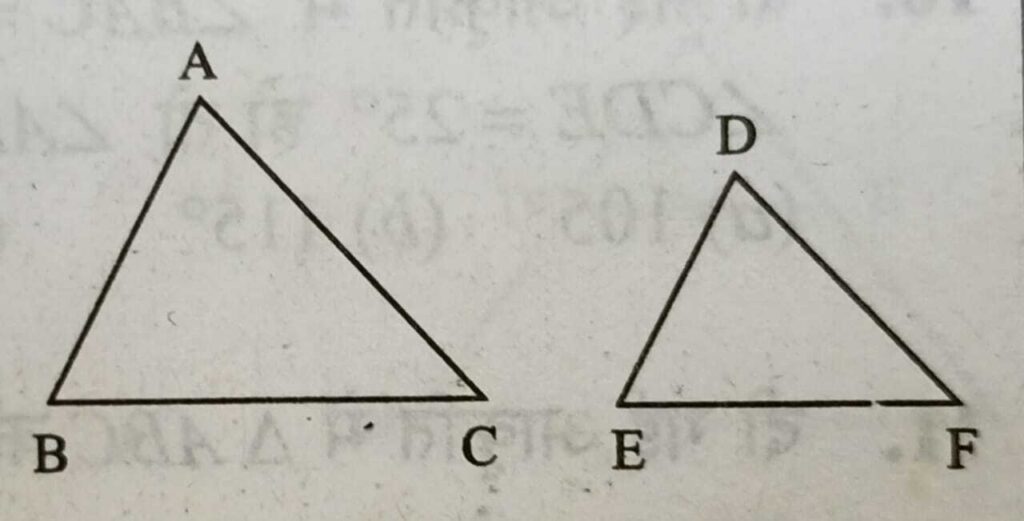
त्रिभुज की सर्वांगसमता के नियम :-

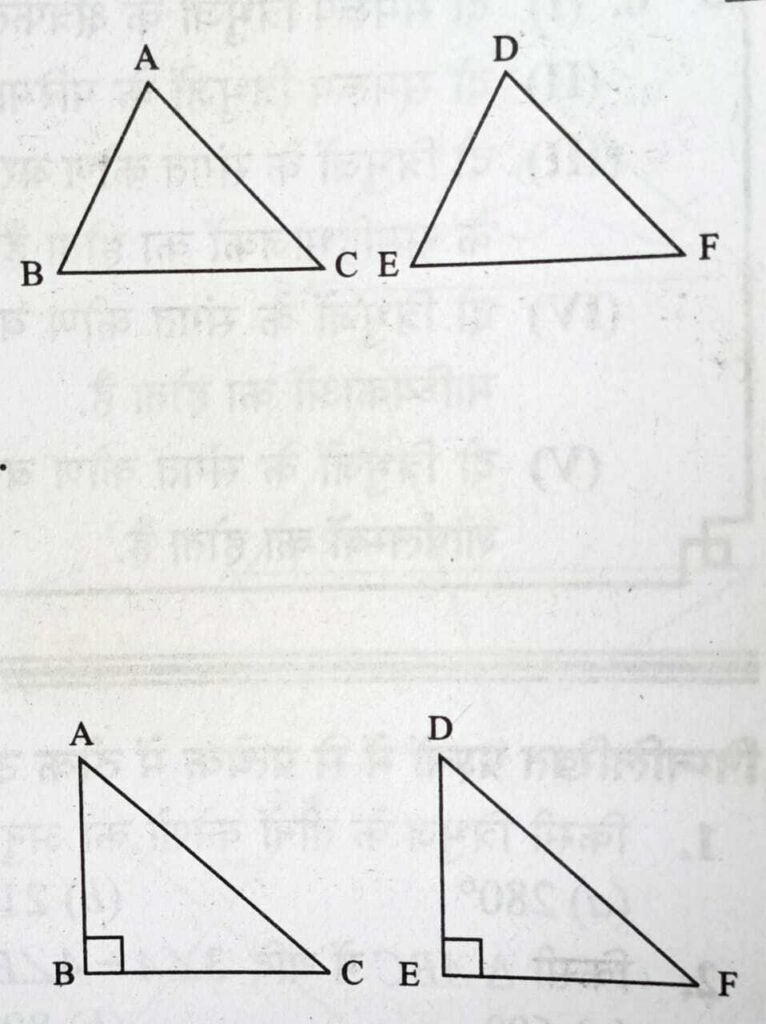
∆ABC ≅ ∆DEF होगा यदि

SAS – Axiom :-

1. AB = DE, BC = EF तथा ∠B = ∠E
2. AB = DE, AC = DF तथा ∠A = ∠D
3. BC = EF, AC = DF तथा ∠C = ∠F

SSS – Axiom :

AB = DC, BC = EF तथा AC = DF

ASA – Axiom :

1. ∠B = ∠E, ∠C = ∠F तथा BC = EF
2. ∠C = ∠F, ∠A = ∠D तथा AC = DF
3. ∠A = ∠D, ∠B = ∠E तथा AB = DE

RHS – Axiom :

∆ABC ≅ ∆DEF होगा यदि

1. ∠B = ∠E = 90, AB = DE, AC = DF
2. ∠B = ∠E = 90, BC = EF, AC = DF

किसी ∆ABC में समान भुजाओ के सम्मुख कोण समान होते है,

1. यदि AB = AC हो, तो ∠C = ∠B
2. यदि AB = BC हो, तो ∠B = ∠A
3. यदि AB = BC हो, तो ∠C = ∠A

किसी ∆ABC में समान कोणों की सम्मुख भुजाये समान होती है

त्रिभुज की समरूपता के नियम :-

थेल का प्रमेय :-

∆ABC में यदि DE ∥ BC हो, तो

1. AD/DB = AE/EC
2. AD/AB = AE/AC
3. AB/DB = AC/EC

किसी त्रिभुज की दो भुजाओ के मध्य बिन्दुओ को मिलाने वाला रेखाखंड तीसरी भुजा के समान्तर तथा इसके आधे के बराबर होता है

त्रिभुज के किसी कोन का समद्विभाज्क उसकी सम्मुख भुजा को शेष दो भुजाओ के अनुपात में विभाजित करता है

1. AAA – समरूपता : यदि ∠A = ∠D, ∠B = ∠E, ∠C = ∠F तथा AB/DE = BC/EF = CA/FD हो, तो ∆ABC ~ ∆DEF
2. AA – समरूपता : यदि ∠A = ∠D तथा ∠B = ∠E, तो ∆ABC ~ ∆DEF
3. SSS – समरूपता : यदि AB/DE = BC/EF = AC/DF हो, तो ∆ABC ~ ∆DEF
4. SAS – समरूपता : यदि ∠A = ∠D तथा AB/DE = AC/DF हो, तो ∆ABC ~ ∆DEF

त्रिभुज की समरूपता से सम्बंधित कुछ अन्य जानकारी

1. दो समरूप त्रिभुजो के क्षेत्रफलो का अनुपात उनकी संगत भुजाओ के वर्गो के अनुपात के बराबर होता है
2. दो समरूप त्रिभुजो के परिमाप का अनुपात उनकी संगत भुजाओ के अनुपात के बराबर होता है
3. दो त्रिभुजो के संगत कोण बराबर हो तो उनकी संगत भुजाओ का अनुपात वही होता है जो की संगत कोणों के सम द्विभाज्क का होता है
4. दो त्रिभुजो के संगत कोन बराबर हो, तो उनकी संगत भुजाओ का अनुपात वही होता है जो कि संगत मध्यिकाओ का होता है
5. दो त्रिभुजो के संगत कोण बराबर हो, तो उनकी संगत भुजाओ का अनुपात वही होता है जो कि संगत शीर्षलम्बो का होता है