Q21. यदि समीकरण x2 – px + q = 0 के मूल α तथा β हो, तो
- (α2 + β2) का मान ज्ञात कीजिए
- (α3 + β3) का मान ज्ञात कीजिए
यदि समीकरण x2 – px + q = 0 के मूल α तथा β हो, तो
दी गई समीकरण की x2 + (α + β)x + αβ = 0 से तुलना करने पर
(α + β) = -p और αβ = q ……………………….1
- (α2 + β2) का मान ज्ञात करने के लिए
(α + β)2 = (-p)2 {∵ दोनों तरफ स्क्वायर करने पर}
(α2 + β2 + 2αβ) = p2
(α2 + β2 + 2q) = p2 {∵ αβ = q }
(α2 + β2) = p2 – 2q
- (α3 + β3) का मान ज्ञात करने के लिए
(α + β)3 = (-p)3 {∵ दोनों तरफ क्यूब करने पर}
(α3 + β3 + 3α2β + 3αβ2) = -p3
(α3 + β3) + 3αβ(α + β) = -p3
(α3 + β3) + 3q(-p) = -p3 {∵ (α + β) = -p और αβ = q}
(α3 + β3) = -(p3 + 3pq)
नीचे दिए गए फोटो में बताए गए द्विघात समीकरण के सूत्रों को आपको भली भांति समझ और याद कर लेना चाहिए तभी आपको नीचे के सवाल समझ में आएगे
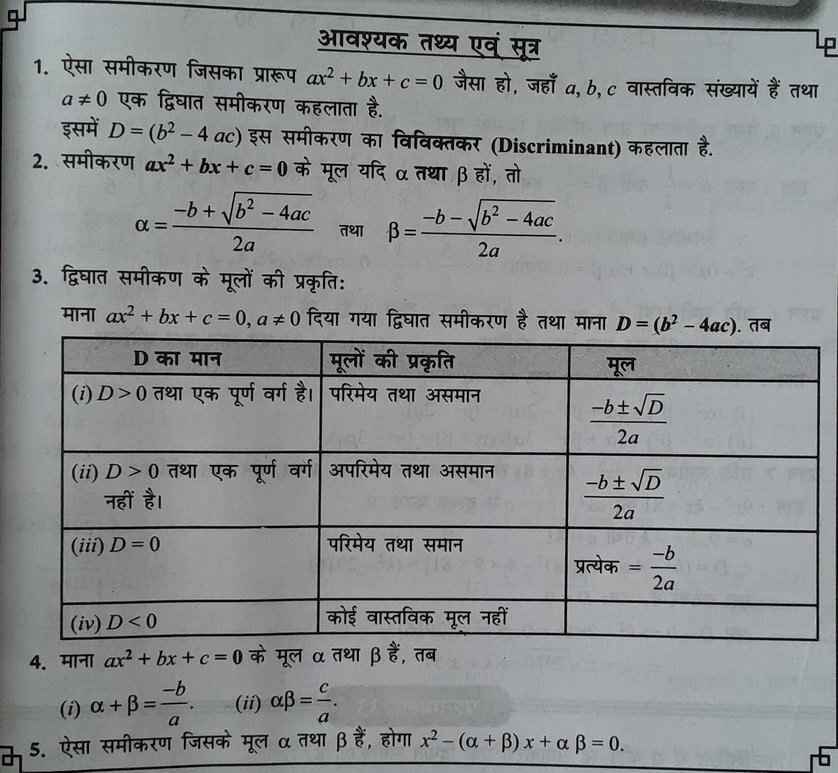
Q22. यदि समीकरण 9x2 – kx + 81 = 0 के मूल बराबर हो, तो k का मान ज्ञात कीजिए ?
किसी भी समीकरण के मूल केवल और केवल तभी बराबर होगे जब विवित्कर D = 0 होगा
∴ D = 0 ⇒ b2 – 4ac = 0 ………………….1
a, b, c की वैल्यू निकलने के लिए हम उपरोक्त दी गई समीकरण की ax2 + bx + c = 0 से तुलना करेगे
a = 9, b = k और c = 81
b2 – 4ac = 0 समीकरण 1 से
k2 – 4×9×81 = 0
k2 – 2916 = 0
k2 = 2916
k = 54
Q23. निम्नलिखित में से कोन-सा समीकरण एक द्विघात समीकरण है ?
- x2 + 3/x2 = 1
- 2x2 – √(3x) + 5 = 0
- x3 – x – 4 = 0
- x2 – 1 = 2x2 + 4
जेसा कि हमने जाना कि द्विघात समीकरण केवल और केवल वही बहुपद होगा जिसके चर (x) की अधिकतम शक्ति 2 हो
∴ आप्शन (4)
x2 – 1 = 2x2 + 4 ⇒ x2 + 5 एक द्विघात समीकरण है
Q24. 2x2 – 7x + 5 = 0 समीकरण के मूल क्या होगे ?
सबसे पहले हमे दो ऐसे अंक फाइंड करने है जिनका जोड़ -7 हो और गुणा 10 हो (गुणा = ac = 2 × 5 = 10)
अंक 10 के गुणनखण्ड = 2×5
∴ अंक -2 और -5 दो ऐसे अंक है जिनका जोड़ -7 है और गुणा 10
2x2 – 7x + 5 = 0
2x2 – 2x – 5x + 5 = 0
2x(x – 1) – 5(x -1) = 0
(2x – 5)(x – 1) = 0
2x – 5 = 0, x – 1 = 0
x = 5/2, x = 1
Q25. द्विघात समीकरण 2x2 – 3x – 12 = 0 का विविक्त्कर कितना है ?
विविक्त्कर निकालने का सूत्र (D) = b2 – 4ac
सबसे पहले हम दी गई समीकरण की ax2 + bx + c = 0 से तुलना करके a, b, c का मान निकालेगे
∴ a = 2, b = -3, c = -12
D = b2 – 4ac = 9 – (-96) = 100
ध्यान दे –
अगर आपको समीकरण आसान और गुणनखण्ड आसानी से मिल जाये तो आप उसमे गुणनखण्ड विधि से मूल निकाल सकते है और अगर समीकरण कुछ अटपटी सी दिखाई दे तो वहा पर विविक्त्कर विधि सर्वश्रेष्ट है जेसे – सवाल नम्बर 7,8 और 9
Q26. समीकरण x2 – 9x + 18 = 0 के मूल है ?
सबसे पहले हमे दो ऐसे अंक फाइंड करने है जिनका जोड़ -9 हो और गुणा 18 हो (गुणा = ac = 1 × 18 = 18)
अंक 18 के गुणनखण्ड = 2×3×3
∴ अंक -6 और -3 दो ऐसे अंक है जिनका जोड़ -9 है और गुणा 18
x2 – 9x + 18 = 0
x2 – 6x – 3x + 18 = 0
x(x – 6) – 3(x – 6) = 0
(x – 3)(x – 6) = 0
(x – 3) = 0, (x – 6) = 0
x = 3, x = 6
Q27. समीकरण 2x2 – 11x + 15 = 0 के मूल है ?
सबसे पहले हमे दो ऐसे अंक फाइंड करने है जिनका जोड़ -11 हो और गुणा 30 हो (गुणा = ac = 2 × 15 = 30)
अंक 30 के गुणनखण्ड = 2×3×5
∴ अंक -6 और -5 दो ऐसे अंक है जिनका जोड़ -11 है और गुणा 30
2x2 – 11x + 15 = 0
2x2 – 6x – 5x + 15 = 0
2x(x – 3) – 5(x – 3) = 0
(2x – 5)(x – 3) = 0
x = 5/2, x = 3
Q28. समीकरण x2 – 4√3x + 9 = 0 के मूल है ?
यह समीकरण हमे कुछ अटपटी सी लग रही है इसलिए हम इसके मूल विविक्त्कर विधि से निकालेगे
विविक्त्कर विधि से मूल निकालने का सूत्र = (-b ± √D) / 2a जहा D = b2 – 4ac है
सबसे पहले हमे a, b, c के मान निकलने होगे इसलिए हम उपरोक्त समीकरण की ax2 + bx + c = 0 से तुलना करेगे
∴ a = 1, b = -4√3, c = 9
D = b2 – 4ac = (4√3)2 – 36 = 48 – 36 = 12
विविक्त्कर विधि से मूल = (-b ± √D) / 2a
= [-(-4√3) ± √12] / 2
= (4√3 + √12) / 2 और (4√3 – √12) / 2
Q29. समीकरण के ax2 + x + b = 0 मूल समान होगे, यदि
(a) b2 = 4a
(b) b2 < 4a
(c) b2 > 4a
(d) ab = 1/4
समीकरण के ax2 + x + b = 0 मूल समान होगे, यदि D = 0
D = b2 – 4ac {By Formula}
सबसे पहले हमे a, b, c के मान निकलने होगे इसलिए हम उपरोक्त समीकरण की ax2 + bx + c = 0 से तुलना करेगे
∴ a = a, b = 1, c = b
0 = (1)2 – 4ab
4ab = 1
ab = 1/4
Q30. p के किस मान के लिए समीकरण px2 + 2√5x + 4 = 0 के मूल वास्तविक तथा बराबर होंगे ?
हमे याद है कि किसी भी द्विघात समीकरण के मूल वास्तविक और बराबर तभी होगे जब D = 0 हो
D = b2 – 4ac {By Formula}
सबसे पहले हमे a, b, c के मान निकलने होगे इसलिए हम उपरोक्त समीकरण की ax2 + bx + c = 0 से तुलना करेगे
∴ a = p, b = 2√5, c = 4
0 = (2√5)2 – 16p
16p = 20
p = 5/4



