LCM and HCF in hindi – लघुत्तम और महत्तम समापवर्तक

ल.स. और म.स. पर आधारित प्र्श्नो को LCM and HCF formula and tricks से 43 सवालो को हल किया गया है LCM and HCF in hindi और निम्नलिखित सभी सवालों को ड़ा आर एस अग्रवाल मैथ से उठाए गए है –

LCM and HCF in hindi और LCM and HCF formula and tricks आधारित सवाल :-

(a) गुणनखण्ड तथा गुणज :

यदि a, b को पूर्णतया विभक्त कर दे तो a को b का गुणनखण्ड कहते है तथा b को a का गुणज कहते है

उदाहरण : 7 है 35 का गुणनखण्ड और 35 का गुणज है 7

(b) महत्तम समापवर्तक (म.स.) :

दो या दो से अधिक संख्याओ का म.स. वह बड़ी से बड़ी संख्या है जो प्रत्येक दी गई संख्या को पूर्णतया विभक्त कर दे

जैसे : 56 और 72 का म.स. 8 होगा

(c) लघुत्तम समापवर्त्य (ल.स.) :

वह छोटी से छोटी संख्या जो प्रत्येक दी गई संख्या द्वारा पूर्णतया विभक्त हो जाये, दी गई संख्या का लघुत्तम समापवर्त्य कहलाती है

जैसे : संख्या 7 और 8 का ल.स. 56 होगा

(d) महत्तम समापवर्तक निकालने के दो तरीके

1. अगर किन्ही दो संख्याओ का निकालना हो तो direct विधि
2. और अगर दो से ज्यादा संख्याओ का निकालना हो तो गुणनखण्ड विधि #common factor#

(e) लघुत्तम समापवर्त्य निकालने का सिर्फ एक तरीका

सभी संख्याओ का एक बार ही गुणनखण्ड लेकर #all factor#

(f) दो संख्याओ का गुणनफल = (इनका म.स.) × (इनका ल.स.)

(g) भिन्नों का म.स. = (अंशो का म.स.) / (हरों का ल.स.)

(h) भिन्नों का ल.स. = (अंशो का ल.स.) / (हरों का म.स.)

LCM and HCF formula and tricks आधारित प्रश्न :-

Q1. 368/437 का सरलतम रूप क्या है ?

Ans. 368 तथा 437 का म.स. = 23

(अगर दो संख्याओ का म.स. निकालना हो)

= \frac{368/23}{437/23}

= \frac{16}{19}

Q2. 84, 126, 140 का महत्तम समापवर्तक कितना है ?

संख्या 84, 126 और 140 में से प्रत्येक से गुणनखण्ड लेने पर :

(अगर दो संख्याओ से अधिक का म.स. निकालना हो)

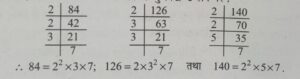
∴ 84 = 2² × 3 × 7; 126 = 2 × 3² × 7 तथा 140 = 2² × 5 × 7

अत 84, 126, 140 का म.स. = ऐसी संख्याये लेंगे जो तीनों संख्याओ के गुणनखण्ड हो

∴ 84, 126, 140 का म.स. = (2 × 7)

Q3. 15, 18, 24, 27, 36 का लघुत्तम समापवर्त्य क्या होगा ?

संक्षिप्त विधि द्वारा :

∴ ल.स. = (3 × 3 × 2 × 2 × 5 × 2 × 3) = 1080

Q4. 1.75, 5.6 तथा 7 का महत्तम समापवर्तक ज्ञात कीजिए

1.75 = 175/100 = 7/4

5.6 = 56/10 = 28/5 तथा

7 = 7/1

अब इनका महत्तम समापवर्तक = (तीनो संख्याओ के अंश का म.स.) / (तीनो संख्याओ के हर का ल.स.)

= (7, 28, 7 का म.स.) / (4, 5, 1 का ल.स.)

= 7 / 20

= 0.35

Q5. 0.36, 1.2, 4.8 का लघुत्तम समापवर्त्य ज्ञात कीजिए ?

0.36 = 36/100 = 9/25

1.2 = 12/10 = 6/5

4.8 = 48/10 = 24/5

अब इनका लघुत्तम समापवर्त्य = (तीनो संख्याओ के अंश का ल.स.) / (तीनो संख्याओ के हर का म.स.)

= (9, 6, 24 का ल.स.) / (25, 5, 5 का म.स.)

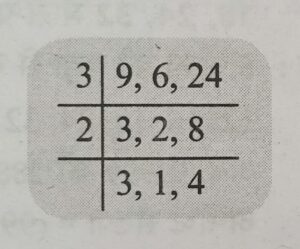
= 72/5

Q6. दो संख्याओ का लघुत्तम समापवर्त्य 1920 तथा महत्तम समापवर्त्य 16 है यदि इनमें से एक संख्या 128 हो, तो दूसरी संख्या क्या होगी ?

माना दूसरी संख्या = a, तब

पहली संख्या × दूसरी संख्या = ल.स.× म.स.

128a = 1920 × 16

a = (1920 × 16) / 128

a = 240

Q7. वह दो से छोटी संख्या कौन-सी है जो 8, 12, 18, 24 में से प्रत्येक से पूर्णतया विभक्त हो जाये ?

उपोक्त संख्याओ का हमे ल.स. निकालना होगा क्योकि केवल और केवल ल.स. ही वह छोटी से छोटी संख्या होगी जो उपरोक्त सभी से पूर्णतया विभक्त हो जाये

∴ ल.स. = (2 × 2 × 2 × 3 × 3)

= 72

Q8. वह छोटी से छोटी संख्या कौन-सी है जिसे 14, 21, 28, 35 में से प्रत्येक से भाग देने पर प्रत्येक दशा में 5 शेष बचे ?

[उपोक्त संख्याओ का ल.स. + 5] वह संख्या होगी जिसे बताई गई संख्या से भाग देने पर हर दशा में 5 शेष बचेगा

∴ अभीष्ट संख्या = [14, 21, 28, 35 का ल.स. + 5]

= [(2 × 7 × 3 × 2 × 5) + 5]

= [420 + 5]

= 425

Q9. वह छोटी से छोटी संख्या ज्ञात करो जिसमें से 8 घटाने पर शेष बची संख्या 16, 18, 20, 24 में से प्रत्येक से पूर्णतया विभक्त हो जाये

[उपोक्त संख्याओ का ल.स. + 8] वह संख्या होगी जिसे बताई गई संख्या से भाग देने पर पूर्णतया विभक्त होगी

∴ अभीष्ट संख्या = [16, 18, 20, 24 का ल.स. + 8]

= [(2 × 2 × 2 × 3 × 2 × 3 × 5) + 8]

= [720 + 8]

= 728

Q10. वह छोटी से छोटी संख्या ज्ञात करो जिसे 20, 25 तथा 30 से भाग देने पर क्रमशः 8, 13 तथा 18 शेष बचे

20, 25 तथा 30 से भाग देने पर क्रमशः 8, 13 तथा 18 शेष बचे ⇒ मतलब प्रत्येक से 12 बचे

[उपोक्त संख्याओ का ल.स. – 12] वह अभीष्ट संख्या होगी  {👈 ध्यान दे}

∴ अभीष्ट संख्या = [20, 25, 30 का ल.स. – 12]

= [(5 × 2 × 2 × 5 × 3) – 12]

= 288